Ecuaciones de estado

Publicado el 1 de febrero por Richard  ‐ 2 min. de lectura

Las ecuaciones de estado modelan el comportamiento de una sustancia y se pueden representar de la siguiente manera:

$$ \begin{align} f(p,V,T)=0 \end{align} $$

donde:

• $p$ es la presión.
• $V$ es el volumen.
• $T$ es la temperatura.

Ecuación de estado térmica#

Partiendo de la ley de gas ideal:

$$ \begin{align} p=\dfrac{n RT}{V} \end{align} $$

la cual podemos expresar de la siguiente forma:

$$ \begin{align} pV=nRT \end{align} $$

la cual es conocida como ecuación de Clapeyron-Mendeleiev. Donde:

$$ \begin{align} n=\dfrac{m}{M}=\dfrac{\text{masa de la sustancia}}{\text{masa molar}} \end{align} $$

Ecuación de estado calórica#

La ecuación de estado calórica se expresa de la siguiente forma:

$$ \begin{align} U=U_0+C_v(T-T_0) \end{align} $$

esta ecuación se demostrará mas adelante.

• $U$ es la energía interna.
• $C_v$ es la capacidad calorífica a $V=cte$.

Procesos Termodinámicos#

• Isotérmico ($T=cte$).
• Isobárico ($p=cte$).
• Isocórico ($V=cte$).
• Politrópico ($C=cte$).
• Adiabático $\left(C=\dfrac{\delta Q}{dT}=0\right)$.

Proceso Isotérmico (T=cte)#

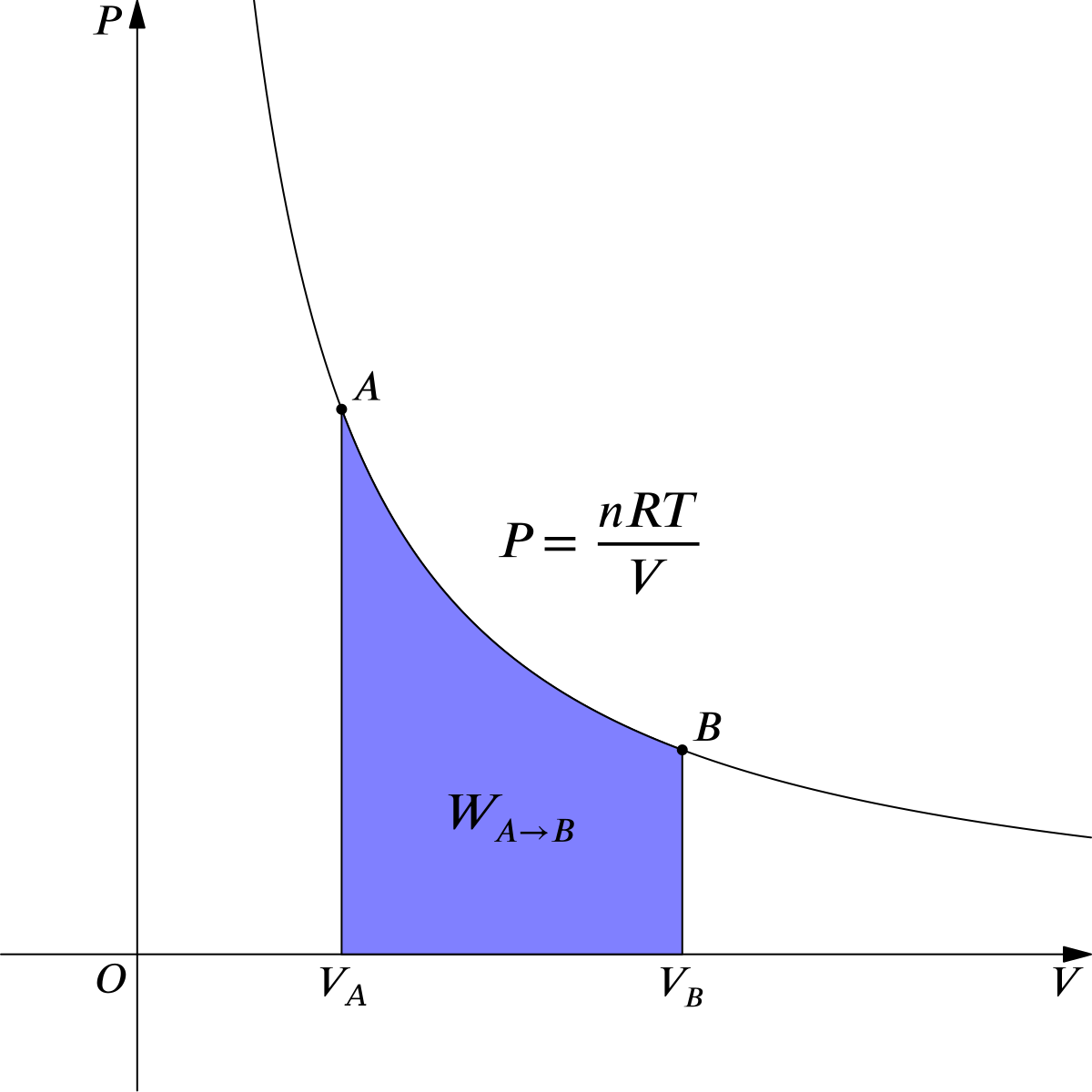
Partiendo de la ecuación de Clapeyron-Mendeleiev, como $T=cte$ entonces $nRT=c_1$

$$ \begin{align} pV=nRT=c_1 \end{align} $$

De modo que:

$$ \begin{align} pV=c_1 \rightarrow p=\dfrac{c_1}{V}=p(V) \end{align} $$

donde $c_1=nRT$.

Proceso Isobárico (p=cte)#

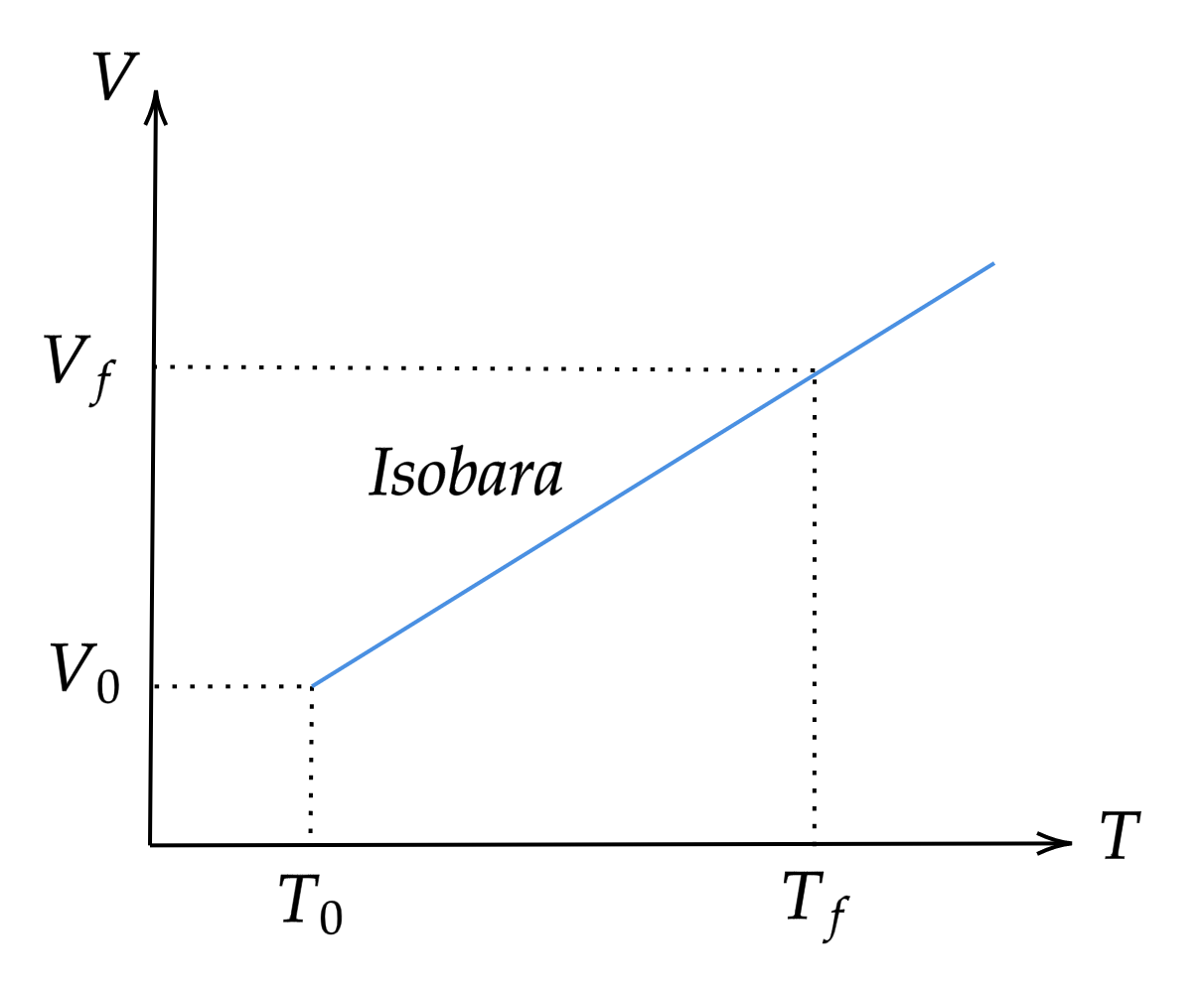
Partiendo de la ecuación de Clapeyron-Mendeleiev, como $p=cte$ entonces:

$$ \begin{align} pV=nRT \rightarrow V=\dfrac{nRT}{p} \end{align} $$

donde $\dfrac{nR}{p}=cte=c_2$, entonces:

$$ \begin{align} V=\dfrac{nRT}{p}=c_2 T=V=f(T) \end{align} $$

Proceso Isocórico#

Partiendo de la ecuación de Clapeyron-Mendeleiev, como $V=cte$ entonces:

$$ \begin{align} pV=nRT \rightarrow p=\dfrac{nRT}{V} \end{align} $$

donde $\dfrac{nR}{V}=cte=c_3$, entonces:

$$ \begin{align} p=\dfrac{nRT}{V}=c_3 T=f(T) \end{align} $$